Was ist ein Spannbaum?
Ein Spannbaum ist in der Graphentheorie ein Teilgraph eines ungerichteten Graphen, der ein Baum ist und alle Knoten dieses Graphen enthält.
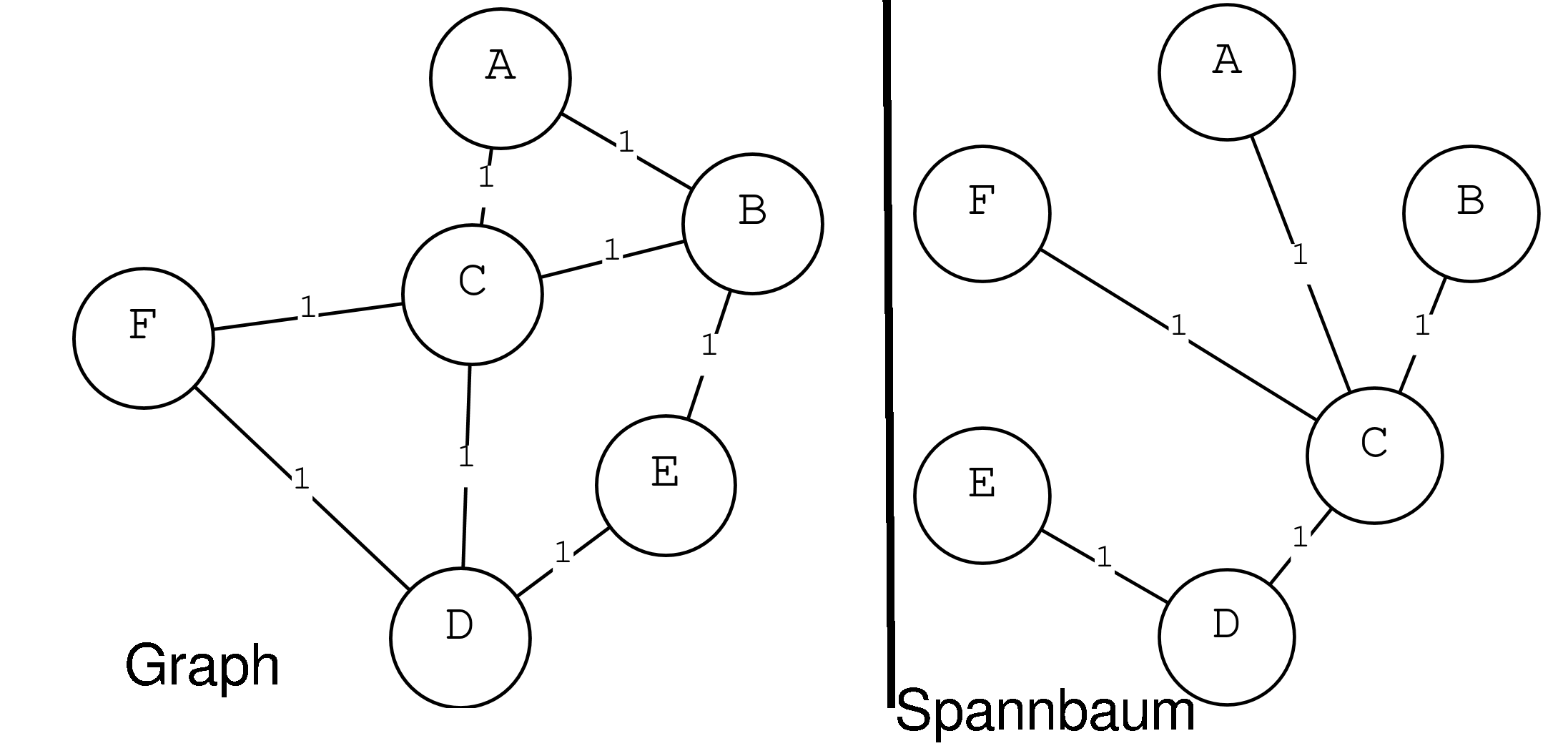
- Ein Graph kann mehrere Spannbäume haben.
- So kann ein vollständiger Graph nach dem Satz von Cayley bis zu n^(n-2) Spannbäume haben.
- Ebenfalls hat jeder zusammenhängende Graph mindesten einen Spannbaum, da man von jedem Knoten über (Um)-Wege jeden anderen Knoten erreichen kann. Somit kann man über diese Verbindungen einen Baum erzeugen. Man kann einen Spannbaum z.B über die Breitesuche oder Tiefensuche erzeugen
Breitensuche
Bei der Breitensuche geht man von einem Startknoten aus und geht dann von diesem nacheinander alle Kinderknoten ab. Nachdem diese Kinderknoten abgesucht werden, werden deren Kinder abgesucht und so weiter. Der Rekursive Algorithmus in Java implementiert und mit einer Queue relativ trivial implementiert. Jeder noch abzulaufende Knoten wird einfach zu der Queue hinzugefügt.
public Graph breitensuche(Graph pGraph, Vertex pStart, Vertex pZiel) { if ((pGraph == null) || (pStart == null)) { return null; } pGraph.setAllVertexMarks(false); pGraph.setAllEdgeMarks(false); Graph res = new Graph(); Queue<Vertex> q = new Queue(); pStart.setMark(true); if (pStart.getID().equals(pZiel.getID())){ res.addVertex(pStart); return res; } q.enqueue(pStart); res.addVertex(pStart); tfBreitendurchlauf.setText(pStart.getID()); while (!q.isEmpty()) { Vertex v = q.front(); q.dequeue(); List<Vertex> neighbours = pGraph.getNeighbours(v); neighbours.toFirst(); while (neighbours.hasAccess()) { Vertex n = neighbours.getContent(); if(!n.isMarked()) { n.setMark(true); res.addVertex(n); res.addEdge(new Edge(v, n, 1)); q.enqueue(n); } if(n.getID().equals(pZiel.getID())) { return res; } neighbours.next(); } } return res; }
Tiefensuche
In der Tiefensuche werden zuerst alle Kinder und dessen ersten Kindes eines Startknoten abgelaufen bevor das nächste Kind abgesucht wird. Rekursiv ist die Implementierung recht simpel.
public Graph tiefensucheRek(Graph g, Vertex start, Vertex ziel) { Graph res = new Graph(); g.setAllVertexMarks(false); g.setAllEdgeMarks(false); start.setMark(true); res.addVertex(start); tiefenSchritt(g, start, ziel, res); return res; } public void tiefenSchritt(Graph g, Vertex v, Vertex end, Graph res) { if(v.getID().equals(end.getID())) return; List<Vertex> neighbours = graph.getNeighbours(v); neighbours.toFirst(); while (neighbours.hasAccess()) { Vertex n = neighbours.getContent(); if(!n.isMarked()) { n.setMark(true); res.addVertex(n); res.addEdge(new Edge(v, n, 1)); tiefendurchlauf(pGraph, n, end, res); } neighbours.next(); } }
Minimaler Spannbaum
Wenn man einen Graphen mit gewichteten Kanten hat, dann kann man bei der Erstellung des Spannbaumes die Summe der Gewichte der benutzten Kanten nehmen.
Diese Summe nennt man das Gewicht des Spannbaumes.
Daher ist ein minimaler Spannbaum ein Spannbaum eines Graphen mit der minimalen Summe der Kantengewichte.

Der Algorithmus von Prim
Schon in 1930 hat der Tschechische Mathematiker Jarkník den Algorithmus gefunden, welcher von Prim in 1957 bekannt gemacht wurde. Dieser geht folgendermaßen vor:
- Man wählt einen beliebigen Knoten als Startknoten und fügt diesen zum Ergebnissgraphen hinzu
- Man wählt die Kante mit dem geringsten Gewicht, welche einen Knoten des Ergebnisgraphen mit einem noch nicht entdeckten Knoten verbindet.
- Man fügt die Kante und den Knoten zum Ergebnisgraphen hinzu
- Dies führt man solange durch, bis alle Knoten entdeckt sind.
Man könnte das ganze in Pseudocode folgendermaßen notieren
Markiere Startknoten V
Füge V zum Ergebnisgraphen E hinzu
Solange noch nicht alle Knoten markiert
Kante K mit kleinstem Gewicht zu unmarkiertem Knoten U
Markiere K und U
Füge K und U zu E hinzu
Dieser Algorithmus findet immer einen minimalen Spannbaum, da es auch mehrere geben kann. Ein Nachteil ist, dass dieser Algorithmus bei einem nicht-zusammenhängenden Graphen nicht terminiert und nicht funktioniert. Prim startet also bei einem Startknoten und arbeitet sich von diesem Graphen stück-für-Stück weiter vor und erweitert immer weiter den Graphen, bis alle Knoten enthalten sind. Allerdings ist der Ansatz sehr intuitiv, genauso wie die Implementierung in Java.
Graph res = new Graph(); BinarySearchTree<EdgeEntry> to_discover = new BinarySearchTree(); graph.setAllEdgeMarks(false); graph.setAllVertexMarks(false); // Die Kanten des Start-Vertex zur Queue hinzufügen Vertex start = graph.getVertices().getContent(); start.setMark(true); res.addVertex(start); List<Edge> start_edges = graph.getEdges(start); start_edges.toFirst(); while(start_edges.hasAccess()) { to_discover.insert(new EdgeEntry(start_edges.getContent())); start_edges.next(); } while(!graph.allVerticesMarked()) { // Die Kante mit dem geringsten Gewicht rausziehen EdgeEntry entry = getMin(to_discover); to_discover.remove(entry); Edge e = entry.e; Vertex v1 = e.getVertices()[0]; Vertex v2 = e.getVertices()[1]; Vertex to_add = !v1.isMarked() ? v1 : v2; if(!v1.isMarked() || !v2.isMarked()) { to_add.setMark(true); res.addVertex(to_add); e.setMark(true); res.addEdge(e); // Alle Kanten des neu gefundenen Knotens hinzufügen List<Edge> edges = graph.getEdges(to_add); edges.toFirst(); while(edges.hasAccess()) { to_discover.insert(new EdgeEntry(edges.getContent())); edges.next(); } } }
Der Algorithmus von Kruskal
1956 hat Joseph Kruskal einen weiteren Weg veröffentlicht einen minimalen Spannbaum eines Graphen zu erstellen. Dazu hat er den folgenden Pseudocode
Probiere solange wie möglich
Markiere von den noch nicht markierten Kanten die Kante mit dem geringsten Gewicht, welche auch keinen Kreis bildet
Oder auch:
V = ungenutzte Knoten
E = ungenutzte Kanten
MST = Neue Kanten (Leer)
sortiere E aufsteigend
für jede Kante e in E:
entferne aus E
wenn MST mit e keine Kreise enthält:
Füge e zu MST hinzu
Dadurch werden zuerst aller kleinen Kanten hinzugefügt und später die immer längeren. Sobald ein Kreis entstehen würde, wissen wir, dass wir diese Kante nicht brauchen würden, da wir alle beteiligten Knoten schon im Baum verbunden haben. Dadurch baut er einen Spannbaum Stück für Stück auf, bis er alle Knoten enthält. Dies berücksichtigt auch nicht-zusammenhängende Graphen, da er keinen Start-Knoten hat und damit unabhängig von der existierenden Verbindungen im Graphen versucht den Ergebnisgraphen zu bauen. Ebenfalls muss der Ergebnisgraph vor vollendung des Algorithmus nicht zusammenhängend sein. Es kann sein, dass sich an verschiedenen Stellen verschiedenen Kanten hinzufügen, bis diese irgendwann verbunden werden.
